- 
+ 
-
+Tutorial: Introductory Tutorial: Physics Informed Neural Networks with PINA¶
--⚠️ Before starting:¶
We assume you are already familiar with the concepts covered in the Getting started with PINA tutorials. If not, we strongly recommend reviewing them before exploring this advanced topic.
-
In this tutorial, we will demonstrate a typical use case of PINA for Physics Informed Neural Network (PINN) training. We will cover the basics of training a PINN with PINA, if you want to go further into PINNs look at our dedicated tutorials on the topic.
-Let's start by importing the useful modules:
-## routine needed to run the notebook on Google Colab
-try:
- import google.colab
-
- IN_COLAB = True
-except:
- IN_COLAB = False
-if IN_COLAB:
- !pip install "pina-mathlab[tutorial]"
-
-import warnings
-import torch
-import matplotlib.pyplot as plt
-
-from pina import Trainer, Condition
-from pina.problem import SpatialProblem
-from pina.operator import grad
-from pina.solver import PINN
-from pina.model import FeedForward
-from pina.optim import TorchOptimizer
-from pina.domain import CartesianDomain
-from pina.callback import MetricTracker
-from pina.equation import Equation, FixedValue
-
-warnings.filterwarnings("ignore")
-Build the problem¶
We will use a simple Ordinary Differential Equation as pedagogical example:
-$$ -\begin{equation} -\begin{cases} -\frac{d}{dx}u(x) &= u(x) \quad x\in(0,1)\\ -u(x=0) &= 1 \\ -\end{cases} -\end{equation} -$$
-with the analytical solution $u(x) = e^x$.
-The PINA problem is easly written as:
-def ode_equation(input_, output_):
- u_x = grad(output_, input_, components=["u"], d=["x"])
- u = output_.extract(["u"])
- return u_x - u
-
-
-class SimpleODE(SpatialProblem):
-
- output_variables = ["u"]
- spatial_domain = CartesianDomain({"x": [0, 1]})
-
- domains = {
- "x0": CartesianDomain({"x": 0.0}),
- "D": spatial_domain,
- }
-
- conditions = {
- "bound_cond": Condition(domain="x0", equation=FixedValue(1.0)),
- "phys_cond": Condition(domain="D", equation=Equation(ode_equation)),
- }
-
- def solution(self, pts):
- return torch.exp(pts.extract(["x"]))
-
-
-problem = SimpleODE()
-We are going to use latin hypercube points for sampling. We need to sample in all the conditions domains. In our case we sample in domain D and x0:
# sampling for training
-problem.discretise_domain(1, "lh", domains=["x0"])
-problem.discretise_domain(20, "lh", domains=["D"])
-Generate data¶
Data for training can come in form of direct numerical simulation results, or points in the domains. In case we perform unsupervised learning, we just need the collocation points for training, i.e. points where we want to evaluate the neural network. Sampling point in PINA is very easy, here we show three examples using the .discretise_domain method of the AbstractProblem class.
# sampling 20 points in [0, 1] through discretization in all locations
-problem.discretise_domain(n=20, mode="grid", domains="all")
-
-# sampling 20 points in (0, 1) through latin hypercube sampling in D, and 1 point in x0
-problem.discretise_domain(n=20, mode="latin", domains=["D"])
-problem.discretise_domain(n=1, mode="random", domains=["x0"])
-
-# sampling 20 points in (0, 1) randomly
-problem.discretise_domain(n=20, mode="random")
-We are going to use latin hypercube points for sampling. We need to sample in all the conditions domains. In our case we sample in D and x0.
# sampling for training
-problem.discretise_domain(1, "random", domains=["x0"])
-problem.discretise_domain(20, "lh", domains=["D"])
-To visualize the sampled points we can use matplotlib.pyplot:
for location in problem.input_pts:
- coords = (
- problem.input_pts[location].extract(problem.spatial_variables).flatten()
- )
- plt.scatter(coords, torch.zeros_like(coords), s=10, label=location)
-_ = plt.legend()
-
-Easily solve a Physics Problem with three step pipeline¶
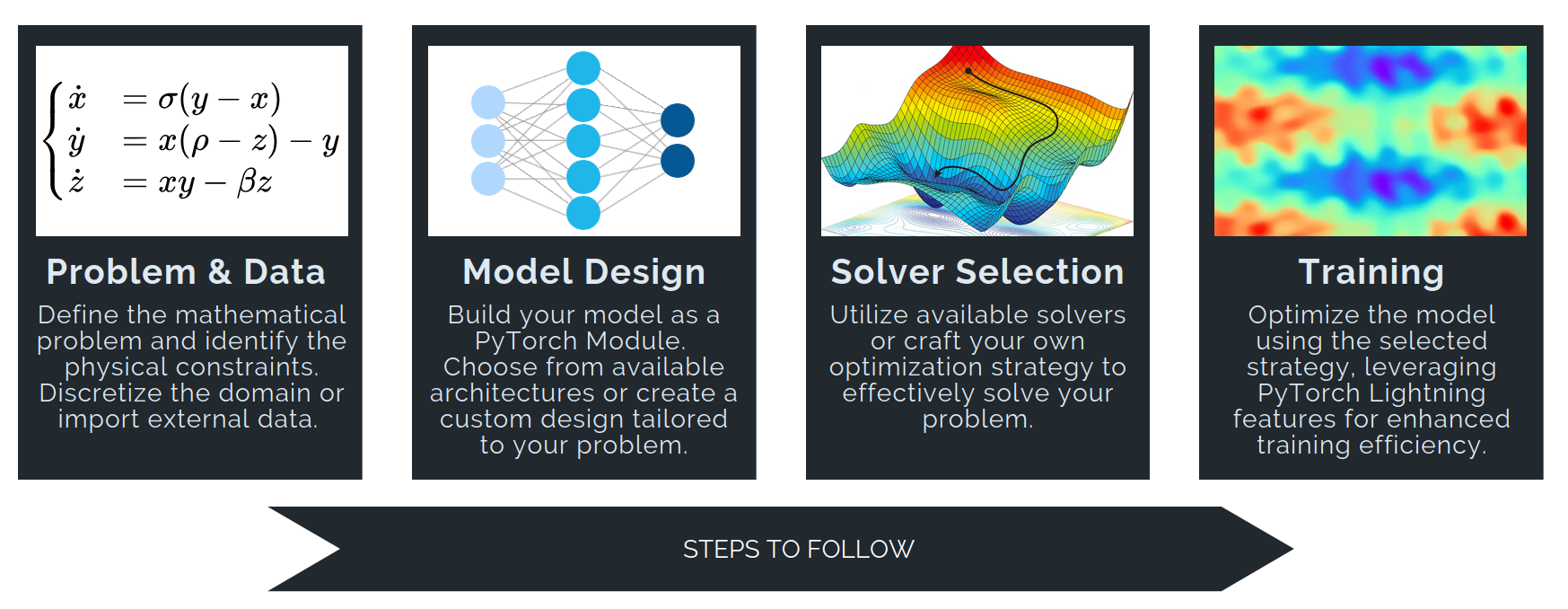
-Once the problem is defined and the data is generated, we can move on to modeling. This process consists of three key steps:
-Choosing a Model
--
-
- Select a neural network architecture. You can use the model we provide in the
pina.modelmodule (see here for a full list), or define a custom PyTorch module (more on this here).
-
Choosing a PINN Solver & Defining the Trainer
--
-
- Use a Physics Informed solver from
pina.solvermodule to solve the problem using the specified model. We have already implemented most State-Of-The-Arte solvers for you, have a look if interested. Today we will use the standardPINNsolver.
-
Training
--
-
- Train the model with the
Trainerclass. The Trainer class provides powerful features to enhance model accuracy, optimize training time and memory, and simplify logging and visualization, thanks to PyTorch Lightning's excellent work, see our dedicated tutorial for further details. By default, training metrics (e.g., MSE error) are logged using a lightning logger (CSVLogger). If you prefer manual tracking, usepina.callback.MetricTracker.
-
Let's cover all steps one by one!
-First we build the model, in this case a FeedForward neural network, with two layers of size 10 and hyperbolic tangent activation:
-# build the model
-model = FeedForward(
- layers=[10, 10],
- func=torch.nn.Tanh,
- output_dimensions=len(problem.output_variables),
- input_dimensions=len(problem.input_variables),
-)
-Then we build the solver. The Physics-Informed Neural Network (PINN) solver class needs to be initialised with a model and a specific problem to be solved. They also take extra arguments, as the optimizer, scheduler, loss type and weighting for the different conditions which are all set to their defualt values.
--💡Bonus tip:¶
All physics solvers in PINA can handle both forward and inverse problems without requiring any changes to the model or solver structure! See our tutorial of inverse problems for more infos.
-
# create the PINN object with RAdam Optimizer, notice that Optimizer need to
-# be wrapped with the pina.optim.TorchOptimizer class
-pinn = PINN(problem, model, TorchOptimizer(torch.optim.RAdam, lr=0.005))
-Finally, we train the model using the Trainer API. The trainer offers various options to customize your training, refer to the official documentation for details. Here, we highlight the MetricTracker from pina.callback, which helps track metrics during training. In order to train just call the .train() method.
--⚠️ Important Note:¶
In PINA you can log metrics in different ways. The simplest approach is to use the
-MetricTrakerclass frompina.callbacksas we will see today. However, expecially when we need to train multiple times to get an average of the loss across multiple runs, we suggest to uselightning.pytorch.loggers(see here for reference).
# create the trainer
-trainer = Trainer(
- solver=pinn, # The PINN solver to be used for training
- max_epochs=1500, # Maximum number of training epochs
- logger=True, # Enables logging (default logger is CSVLogger)
- callbacks=[MetricTracker()], # Tracks training metrics using MetricTracker
- accelerator="cpu", # Specifies the computing device ("cpu", "gpu", ...)
- train_size=1.0, # Fraction of the dataset used for training (100%)
- test_size=0.0, # Fraction of the dataset used for testing (0%)
- val_size=0.0, # Fraction of the dataset used for validation (0%)
- enable_model_summary=False, # Disables model summary printing
-)
-
-# train
-trainer.train()
-💡 Tip: For seamless cloud uploads and versioning, try installing [litmodels](https://pypi.org/project/litmodels/) to enable LitModelCheckpoint, which syncs automatically with the Lightning model registry. --
GPU available: False, used: False --
TPU available: False, using: 0 TPU cores --
`Trainer.fit` stopped: `max_epochs=1500` reached. --
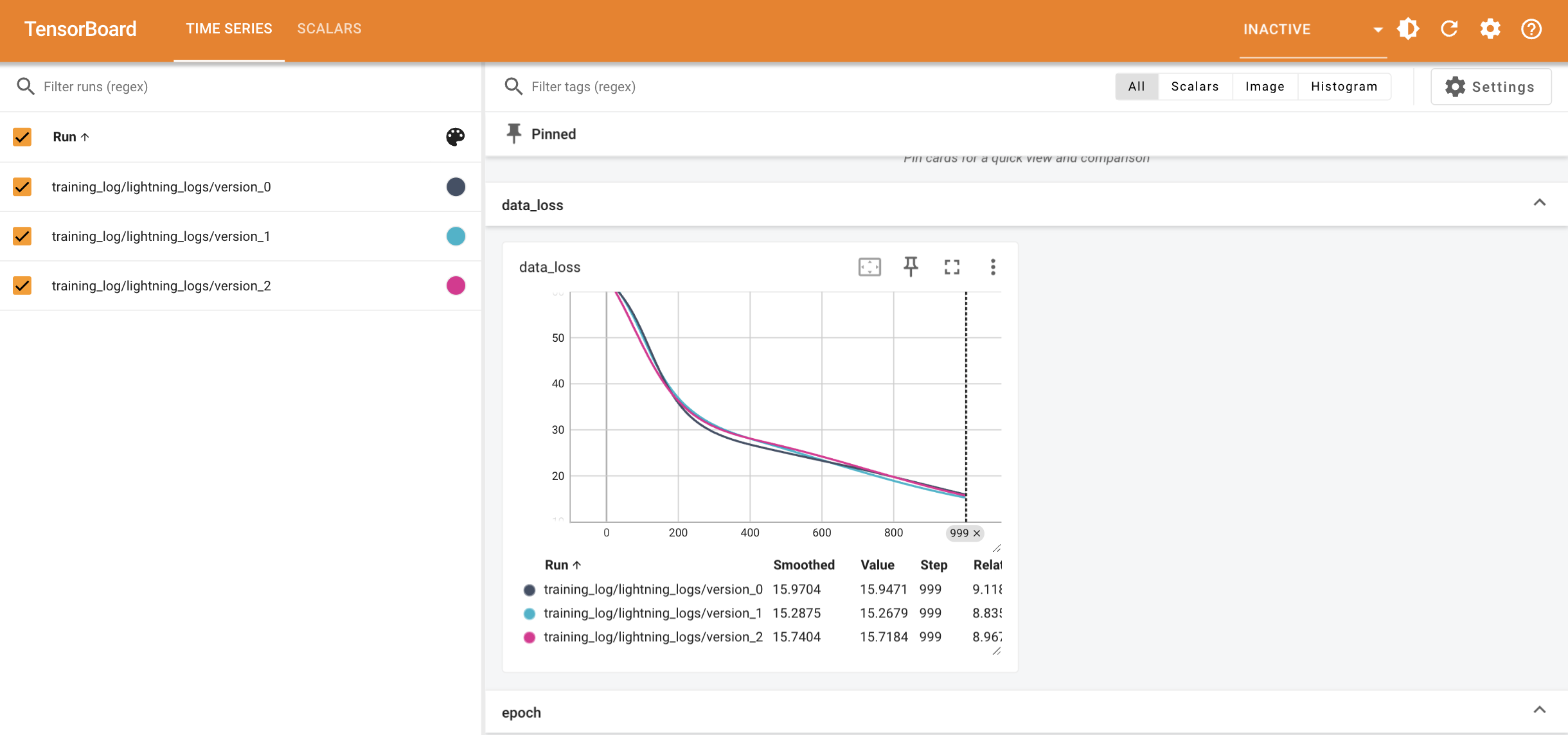
After the training we can inspect trainer logged metrics (by default PINA logs mean square error residual loss). The logged metrics can be accessed online using one of the Lightning loggers. The final loss can be accessed by trainer.logged_metrics
# inspecting final loss
-trainer.logged_metrics
-{'bound_cond_loss': tensor(4.3695e-08),
- 'phys_cond_loss': tensor(1.2907e-05),
- 'train_loss': tensor(1.2950e-05)}
-By using matplotlib we can also do some qualitative plots of the solution.
pts = pinn.problem.spatial_domain.sample(256, "grid", variables="x")
-predicted_output = pinn.forward(pts).extract("u").tensor.detach()
-true_output = pinn.problem.solution(pts).detach()
-fig, ax = plt.subplots(nrows=1, ncols=1)
-ax.plot(pts.extract(["x"]), predicted_output, label="Neural Network solution")
-ax.plot(pts.extract(["x"]), true_output, label="True solution")
-_ = plt.legend()
-
-The solution is overlapped with the actual one, and they are barely indistinguishable. We can also visualize the loss during training using the MetricTracker:
# plot loss
-trainer_metrics = trainer.callbacks[0].metrics
-loss = trainer_metrics["train_loss"]
-epochs = range(len(loss))
-plt.plot(epochs, loss.cpu())
-# plotting
-plt.xlabel("epoch")
-plt.ylabel("loss")
-plt.yscale("log")
-
-What's Next?¶
Congratulations on completing the introductory tutorial on Physics-Informed Training! Now that you have a solid foundation, here are several exciting directions you can explore:
--
-
Experiment with Training Duration & Network Architecture: Try different training durations and tweak the network architecture to optimize performance.
-
-Explore Other Models in
-pina.model: Check out other models available inpina.modelor design your own custom PyTorch module to suit your needs.
-Run Training on a GPU: Speed up your training by running on a GPU and compare the performance improvements.
-
-Test Various Solvers: Explore and evaluate different solvers to assess their performance on various types of problems.
-
-... and many more!: The possibilities are vast! Continue experimenting with advanced configurations, solvers, and other features in PINA.
-
-
For more resources and tutorials, check out the PINA Documentation.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-